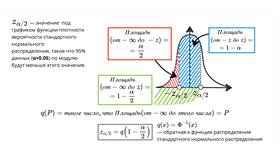
Доверительная вероятность - это статистический показатель, определяющий вероятность того, что доверительный интервал содержит истинное значение оцениваемого параметра. Рассмотрим методы определения и применения этого важного статистического понятия.
Содержание
- 1. Понятие доверительной вероятности
- 2. Стандартные значения доверительной вероятности
- 3. Алгоритм задания доверительной вероятности
- 4. Факторы выбора доверительной вероятности
- 5. Практические примеры
- 6. Расчет в статистических пакетах
- 7. Ошибки при задании доверительной вероятности
- 8. Интерпретация результатов
1. Понятие доверительной вероятности
| Термин | Определение |
| Доверительная вероятность (γ) | Вероятность, с которой доверительный интервал накрывает истинное значение параметра |
| Уровень значимости (α) | Вероятность ошибки, α = 1 - γ |
| Доверительный интервал | Диапазон значений, содержащий истинный параметр с заданной вероятностью |
2. Стандартные значения доверительной вероятности
- 90% (α=0,10) - предварительные исследования
- 95% (α=0,05) - стандартное значение для большинства научных работ
- 99% (α=0,01) - высоконадежные исследования
- 99,9% (α=0,001) - критические приложения
3. Алгоритм задания доверительной вероятности
3.1. Для нормального распределения
- Выберите уровень доверительной вероятности (γ)
- Определите соответствующее значение z-критерия:
- 90% → z=1,645
- 95% → z=1,960
- 99% → z=2,576
- Рассчитайте стандартную ошибку (SE)
- Постройте доверительный интервал: X̄ ± z×SE
3.2. Для t-распределения
| Шаг | Действие |
| 1 | Определите число степеней свободы (n-1) |
| 2 | Найдите критическое значение t-критерия по таблице |
| 3 | Рассчитайте стандартную ошибку среднего |
| 4 | Постройте интервал: X̄ ± tкрит×SE |
4. Факторы выбора доверительной вероятности
- Точность: чем выше γ, тем шире интервал
- Объем выборки: большие выборки позволяют использовать более высокие γ
- Риски: важность последствий ошибки
- Отраслевые стандарты: принятые в конкретной научной области
5. Практические примеры
5.1. Медицинские исследования
Используют γ=95% или 99% из-за высоких требований к надежности
5.2. Социологические опросы
Часто применяют γ=95% с указанием погрешности ±3%
5.3. Промышленные испытания
Могут использовать γ=99,9% для критически важных параметров
6. Расчет в статистических пакетах
| Программа | Синтаксис задания γ |
| R | conf.level = 0.95 в t.test() |
| Python (SciPy) | alpha=0.05 в interval() |
| SPSS | Установка в диалоговом окне анализа |
7. Ошибки при задании доверительной вероятности
- Путаница между γ и α
- Использование z-критерия при малых выборках
- Необоснованный выбор слишком высокого или низкого уровня
- Неучет характера распределения данных
8. Интерпретация результатов
При γ=95% корректно говорить: "Мы на 95% уверены, что истинное значение параметра находится в рассчитанном интервале". Неверно интерпретировать это как вероятность нахождения параметра в конкретном интервале.
Правильный выбор доверительной вероятности требует баланса между точностью оценок и практической значимостью результатов. В большинстве исследований оптимальным считается уровень 95%, но окончательное решение должно учитывать специфику конкретной задачи.
