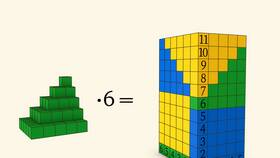Понятие "суммы треугольников" может рассматриваться в разных контекстах математики. Рассмотрим основные интерпретации этого вопроса.
Содержание
Геометрическая интерпретация
В геометрии сумма двух треугольников может пониматься как:
- Объединение их площадей
- Векторная сумма их сторон
- Результат сложения их углов
Сложение площадей треугольников
Если рассматривать сумму как сложение площадей, то:
| Формула | S = S₁ + S₂ |
| Где: | S₁ - площадь первого треугольника S₂ - площадь второго треугольника |
Алгебраическая интерпретация
В алгебре треугольные числа подчиняются следующему правилу сложения:
- n-е треугольное число вычисляется по формуле Tₙ = n(n+1)/2
- Сумма двух треугольных чисел: Tₙ + Tₘ = n(n+1)/2 + m(m+1)/2
Пример вычисления
| Первое треугольное число (T₃) | 1+2+3 = 6 |
| Второе треугольное число (T₄) | 1+2+3+4 = 10 |
| Сумма T₃ + T₄ | 6 + 10 = 16 |
Особые случаи
При сложении конгруэнтных треугольников (равных по форме и размерам) сумма их площадей будет равна удвоенной площади одного треугольника. В векторной алгебре сумма треугольников может образовывать новые геометрические фигуры.